Materi Matematika Matriks Konsep Dasar dan Penerapan

Berita Terkait

Materi matematika matriks akan membahas konsep dasar dan penerapannya dalam matematika. Dari definisi dan jenis-jenis matriks hingga operasi-operasi dan penerapannya dalam berbagai bidang, materi ini akan memberikan pemahaman yang komprehensif.

Materi ini meliputi definisi matriks, jenis-jenisnya, operasi penjumlahan, pengurangan, dan perkalian, serta menghitung determinan dan invers. Pembahasan juga mencakup aplikasi matriks dalam menyelesaikan sistem persamaan linear dan transformasi geometri, serta contoh-contoh soal dan latihan untuk mengasah pemahaman.

Definisi dan Konsep Dasar Matriks

Mengenal Definisi Matriks, Jawaban Latihan A Halaman 129 Nomor 1-3 ...

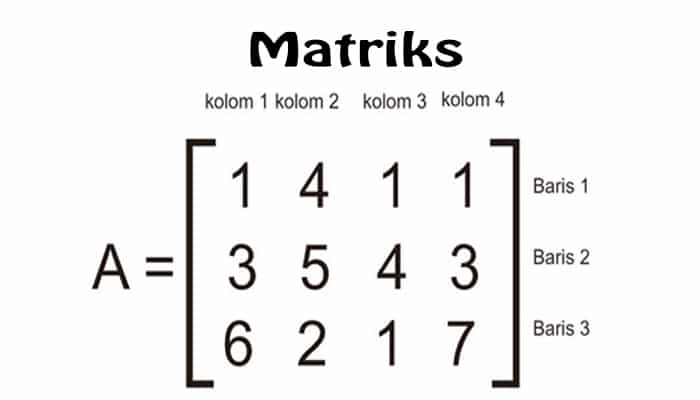
Matriks adalah susunan bilangan yang disusun dalam baris dan kolom membentuk suatu persegi panjang atau persegi. Pemahaman dasar matriks sangat penting dalam berbagai bidang, termasuk matematika, ilmu komputer, dan teknik.

Jenis-Jenis Matriks

Matriks diklasifikasikan berdasarkan jumlah baris dan kolom, serta nilai elemen-elemennya. Berikut beberapa jenis matriks yang umum:

Matriks Baris: Matriks yang hanya memiliki satu baris. Contoh: [1 2 3]
Matriks Kolom: Matriks yang hanya memiliki satu kolom. Contoh:
[4]
[5]
[6]
Matriks Persegi: Matriks yang memiliki jumlah baris sama dengan jumlah kolom. Contoh:
[1 2]
[3 4]
Matriks Nol: Matriks di mana semua elemennya bernilai nol. Contoh:
[0 0]
[0 0]
Matriks Identitas: Matriks persegi di mana elemen-elemen pada diagonal utama bernilai 1, dan elemen lainnya bernilai
0. Matriks identitas sering dilambangkan dengan I. Contoh:
[1 0]
[0 1]

Notasi dan Simbol

Berikut notasi dan simbol yang umum digunakan dalam matriks:

A, B, C: Biasanya digunakan untuk melambangkan matriks.
a_ij: Menyatakan elemen pada baris ke-i dan kolom ke-j dalam matriks A.
Ukuran/Ordo Matriks (m x n): Menunjukkan jumlah baris (m) dan jumlah kolom (n) dalam matriks.

Contoh Matriks

Berikut tabel yang menunjukkan contoh matriks dan jenisnya:

Matriks	Jenis
[1 2 3][4 5 6]	Matriks 2×3
[7][8][9]	Matriks 3×1 (Kolom)
[1 0][0 1]	Matriks 2×2 (Identitas)
[0 0][0 0]	Matriks 2×2 (Nol)

Ilustrasi Visual

Berikut ilustrasi matriks 2×2 dan 3×3 untuk memperjelas konsep:

Matriks 2×2: Susunan bilangan dalam dua baris dan dua kolom. Misalnya, [a b]
[c d].

Matriks 3×3: Susunan bilangan dalam tiga baris dan tiga kolom. Misalnya, [a b c]
[d e f]
[g h i].

Operasi pada Matriks

Setelah memahami konsep dasar matriks, mari kita telusuri berbagai operasi yang dapat dilakukan pada matriks. Pemahaman tentang operasi-operasi ini sangat penting dalam berbagai aplikasi matematika dan ilmu terapan.

Penjumlahan dan Pengurangan Matriks

Penjumlahan dan pengurangan matriks hanya dapat dilakukan pada matriks dengan ukuran yang sama. Elemen-elemen yang bersesuaian dijumlahkan atau dikurangkan. Perhatikan contoh berikut:

Misalnya, kita punya matriks A dan B:

A = [[2, 3], [4, 5]] dan B = [[1, 0], [6, 7]]

Maka penjumlahan matriks A dan B adalah:

A + B = [[3, 3], [10, 12]]

Sedangkan pengurangan matriks A dan B adalah:

A – B = [[1, 3], [-2, -2]]

Perkalian Matriks

Perkalian matriks merupakan operasi yang sedikit berbeda dari penjumlahan dan pengurangan. Perkalian matriks A dan B hanya dapat dilakukan jika jumlah kolom matriks A sama dengan jumlah baris matriks B. Hasil perkalian adalah matriks baru dengan jumlah baris matriks A dan jumlah kolom matriks B. Perhatikan contoh berikut:

Misalkan matriks A berukuran 2×2 dan matriks B berukuran 2×3:

A = [[2, 3], [4, 5]] dan B = [[1, 0, 6], [7, 8, 9]]

Maka perkalian matriks A dan B adalah:

A x B = [[23, 26, 39], [43, 48, 63]]

Untuk menghitung elemen pada baris i dan kolom j dari matriks hasil, kalikan elemen pada baris i dari matriks pertama dengan elemen pada kolom j dari matriks kedua, lalu jumlahkan hasil perkalian tersebut.

Perbandingan Operasi Matriks

Operasi	Syarat	Hasil
Penjumlahan/Pengurangan	Ukuran matriks sama	Matriks dengan ukuran sama
Perkalian	Jumlah kolom matriks pertama sama dengan jumlah baris matriks kedua	Matriks baru dengan jumlah baris matriks pertama dan jumlah kolom matriks kedua

Contoh Perkalian Matriks Numerik

Misalkan kita ingin menghitung perkalian matriks C dan D:

C = [[1, 2], [3, 4]] dan D = [[5, 6], [7, 8]]

Maka perkalian C dan D adalah:

C x D = [[19, 22], [43, 50]]

Ilustrasi Visual Perkalian Matriks

Bayangkan matriks C dan D seperti susunan kotak-kotak. Untuk mendapatkan elemen pada baris pertama kolom pertama dari hasil perkalian, kita ambil baris pertama matriks C dan kolom pertama matriks D. Lalu kalikan elemen-elemen yang bersesuaian dan jumlahkan hasilnya. Proses ini diulang untuk setiap elemen pada hasil perkalian.

Determinan dan Invers Matriks

Setelah memahami operasi dasar pada matriks, kita akan mempelajari cara menentukan nilai determinan dan mencari invers matriks. Kedua konsep ini sangat penting dalam berbagai aplikasi matematika, terutama dalam menyelesaikan sistem persamaan linear.

Determinan Matriks

Determinan matriks adalah sebuah skalar yang dihitung dari elemen-elemen matriks tersebut. Determinan matriks memiliki peran krusial dalam menentukan apakah suatu matriks memiliki invers atau tidak. Matriks yang memiliki determinan nol tidak memiliki invers.

Determinan Matriks 2×2

Rumus perhitungan determinan matriks 2×2 adalah sebagai berikut:

det(A) = ad – bc

dimana A =

Contoh: Jika A = , maka det(A) = (2)(4)
-(3)(1) = 8 – 3 = 5
Determinan Matriks 3×3

Rumus perhitungan determinan matriks 3×3 dapat dihitung dengan ekspansi kofaktor atau dengan metode lainnya. Berikut contoh rumus dengan ekspansi kofaktor:

det(A) = a₁₁(a ₂₂a ₃₃
-a ₂₃a ₃₂)
-a ₁₂(a ₂₁a ₃₃
-a ₂₃a ₃₁) + a ₁₃(a ₂₁a ₃₂
-a ₂₂a ₃₁)

dimana A =

Contoh: Jika A = , maka det(A) = 1((1)(0)
-(4)(6))
-2((0)(0)
-(4)(5)) + 3((0)(6)
-(1)(5)) = 1(0-24)
-2(0-20) + 3(0-5) = -24 + 40 – 15 = 5.

Invers Matriks

Invers matriks adalah matriks yang jika dikalikan dengan matriks aslinya, hasilnya adalah matriks identitas. Invers matriks hanya ada jika determinan matriks tersebut tidak nol.

Mencari Invers Matriks 2×2

Langkah-langkah mencari invers matriks 2×2:
1. Hitung determinan matriks.
2. Tentukan matriks kofaktor.
3. Tentukan matriks adjoint (transpose dari matriks kofaktor).
4. Bagi matriks adjoint dengan determinan matriks.
Contoh: Jika A = , maka A^-1 =
Mencari Invers Matriks 3×3

Langkah-langkah mencari invers matriks 3×3 serupa dengan matriks 2×2, namun lebih kompleks. Gunakan metode adjoin untuk menentukan invers matriks.

Contoh: (Contoh perhitungan invers matriks 3×3 akan membutuhkan ruang yang lebih luas. Sebagai contoh, misalkan A = . Perhitungan inversnya akan menghasilkan matriks A^-1.)

Aplikasi Matriks dalam Matematika

Matriks, sebagai susunan bilangan dalam baris dan kolom, memiliki beragam aplikasi di berbagai bidang, terutama dalam menyelesaikan sistem persamaan linear dan transformasi geometri. Penggunaan matriks juga meluas ke bidang ekonomi dan teknik.

Penerapan Matriks dalam Sistem Persamaan Linear

Matriks menjadi alat ampuh dalam menyelesaikan sistem persamaan linear. Dengan mengubah sistem persamaan menjadi bentuk matriks, solusi dapat ditemukan dengan lebih efisien, terutama untuk sistem persamaan yang kompleks. Contohnya, jika kita memiliki sistem persamaan 2 variabel, kita dapat menuliskannya dalam bentuk matriks koefisien dan variabel, lalu mencari solusi menggunakan operasi matriks.

Penerapan Matriks dalam Transformasi Geometri, Materi matematika matriks

Matriks dapat merepresentasikan transformasi geometri seperti rotasi, refleksi, dan translasi. Transformasi ini dapat diterapkan pada titik-titik dalam bidang koordinat untuk menghasilkan gambar yang diubah. Misalnya, matriks rotasi dapat memutar suatu titik dengan sudut tertentu. Dengan menggunakan matriks, transformasi ini dapat diimplementasikan dengan mudah dan akurat.

Penerapan Matriks dalam Bidang Lain

Penggunaan matriks tak terbatas pada matematika murni. Dalam bidang ekonomi, matriks dapat digunakan untuk memodelkan sistem ekonomi, menganalisis keterkaitan antar sektor, dan menghitung keseimbangan pasar. Dalam teknik sipil, matriks dapat digunakan untuk menganalisis struktur bangunan, menghitung tegangan pada material, dan memodelkan sistem aliran fluida. Penerapannya sangat luas dan terus berkembang seiring dengan perkembangan ilmu pengetahuan dan teknologi.

Contoh Visual Transformasi Geometri

Misalnya, matriks rotasi 90 derajat searah jarum jam dapat ditulis sebagai:

[[0, -1],
[1, 0]]

Matriks ini, ketika dikalikan dengan vektor posisi suatu titik, akan memutar titik tersebut 90 derajat searah jarum jam. Demikian pula, matriks refleksi terhadap sumbu x dapat ditulis sebagai:

[[1, 0],
[0, -1]]

Ringkasan Penerapan Matriks dalam Berbagai Bidang

Bidang	Aplikasi
Matematika	Sistem persamaan linear, transformasi geometri, aljabar linear
Ekonomi	Model ekonomi, analisis input-output, peramalan
Teknik	Analisis struktur, pemodelan sistem, rekayasa kontrol
Komputer Grafis	Animasi, efek visual, rendering

Contoh Soal dan Latihan Operasi Matriks: Materi Matematika Matriks

Berikut disajikan beberapa contoh soal dan latihan untuk memperdalam pemahaman Anda tentang operasi matriks. Contoh-contoh ini mencakup berbagai jenis operasi, mulai dari penjumlahan, pengurangan, hingga perkalian matriks.

Contoh Soal Operasi Matriks

Berikut tabel yang menampilkan contoh soal operasi matriks beserta langkah-langkah penyelesaiannya:

Soal

Langkah Penyelesaian

Solusi

Diketahui matriks A =

[[2, 1],

[3, 4]]

dan matriks B =

[[1, 0],

[0, 2]]

. Tentukan matriks C = A + B.

Menjumlahkan elemen-elemen yang bersesuaian pada matriks A dan B.
C₁₁ = A ₁₁ + B ₁₁ = 2 + 1 = 3
C ₁₂ = A ₁₂ + B ₁₂ = 1 + 0 = 1
C ₂₁ = A ₂₁ + B ₂₁ = 3 + 0 = 3
C ₂₂ = A ₂₂ + B ₂₂ = 4 + 2 = 6
Dengan demikian, matriks C adalah [[3, 1],
[3, 6]]

.

[[3, 1],

[3, 6]]

Diketahui matriks P =

[[5, 2],

[1, 3]]

dan matriks Q =

[[4, 1],

[2, 0]]

. Tentukan matriks R = P – Q.

Mengurangkan elemen-elemen yang bersesuaian pada matriks P dan Q.
R₁₁ = P ₁₁

Q₁₁ = 5 – 4 = 1
R ₁₂ = P ₁₂

Q₁₂ = 2 – 1 = 1
R ₂₁ = P ₂₁

Q₂₁ = 1 – 2 = -1
R ₂₂ = P ₂₂

Q₂₂ = 3 – 0 = 3
Dengan demikian, matriks R adalah [[1, 1],
[-1, 3]]

.

[[1, 1],

[-1, 3]]

Diketahui matriks X =

[[2, 1],

[3, 4]]

dan matriks Y =

[[1, 0],

[0, 2]]

. Tentukan matriks Z = X × Y.

Menggunakan aturan perkalian matriks, kalikan baris matriks X dengan kolom matriks Y.
Z₁₁ = (2 × 1) + (1 × 0) = 2
Z ₁₂ = (2 × 0) + (1 × 2) = 2
Z ₂₁ = (3 × 1) + (4 × 0) = 3
Z ₂₂ = (3 × 0) + (4 × 2) = 8
Dengan demikian, matriks Z adalah [[2, 2],
[3, 8]]

.

[[2, 2],

[3, 8]]

Soal Latihan

Berikut beberapa soal latihan untuk memperdalam pemahaman Anda:

Diketahui matriks A = [[1, 2],
[3, 4]]
dan matriks B =
[[5, 6],
[7, 8]]
. Tentukan matriks C = A + B.
Diketahui matriks P = [[9, 8],
[7, 6]]
dan matriks Q =
[[4, 3],
[2, 1]]
. Tentukan matriks R = P – Q.
Diketahui matriks X = [[1, 2],
[3, 4]]
dan matriks Y =
[[5, 6],
[7, 8]]
. Tentukan matriks Z = X × Y.

Simpulan Akhir

Dengan pemahaman yang baik tentang materi matriks, diharapkan pembaca dapat menerapkannya dalam berbagai konteks matematika dan bidang ilmu lainnya. Semoga materi ini bermanfaat dan dapat memperkaya pengetahuan pembaca tentang konsep matriks.